A recursive function is a function designed to call itself directly or indirectly. Using recursion, a problem can be solved by returning the value call of the same particular function.
A recursive function needs to be terminated at some point. The return of a recursive function is usually based on internal conditions which forwards the logic down to a new iteration until the base case is met.
In recursive functions, the base case is that iteration of a recursive function that does not need an additional recursion to solve a problem.
Base cases are mandatory on recursive functions. Without a base case a recursive function will never terminate leading it to an infinite loop.
Sum all values from 0 to given number and display the result.
function sum(number) {
if (number===0) {
return 0;
}
return number + sum(number-1);
}
sum(10);Sum all even numbers from 0 to given number and display the result.
function sumEven(number) {
if (number===0) {
return 0;
} else if (number%2 !== 0) {
return sumEven(number-1);
}
return number + sumEven(number-1);
}
sumEven(10);Returns the value of exponent operation from given number and grade.
function pow(number, power) {
if (power===1) {
return number;
}
return number * pow(number, power-1);
}
pow(2,2);Returns the product of a given number from 1 to N.
function factorial(number) {
if (number===1) {
return 1;
}
return number*factorial(number-1);
}
factorial(3);Display Pascal’s triangular array of the binomial coefficients.
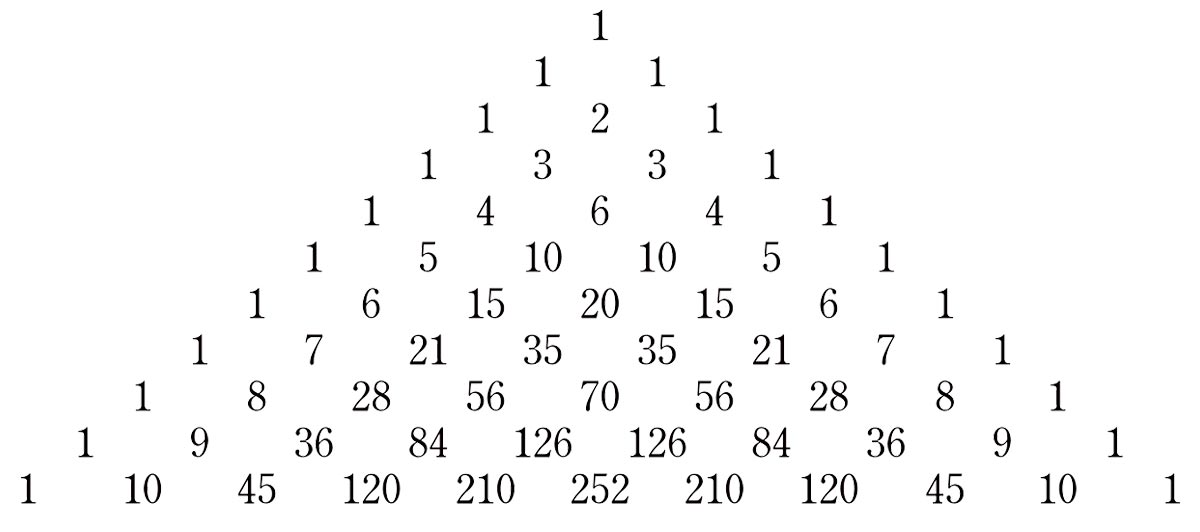
function pascal(row, column) {
if (column>row) {
return 0;
}
if (column<=1 || row<=1) {
return 1;
}
return pascal(row-1, column) + pascal(row-1, column-1);
}
function triangle(number) {
let string = "";
for (let row=1; row<=number; row++) {
for(let column=1; column<=row; column++) {
string += `${pascal(row, column)} `;
}
string += "\n";
}
console.log(string);
}
triangle(10);Displays the Fibonacci sequence from a given number starting with 0.
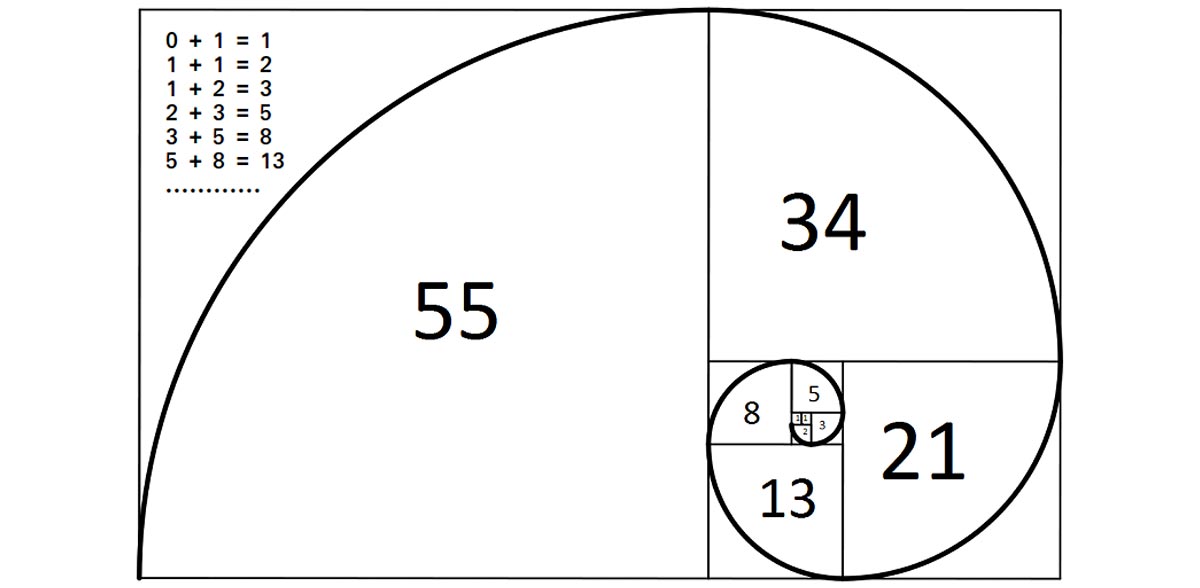
function fib(number) {
function calc(number) {
if (number<=1) {
return number;
}
return calc(number-1) + calc(number-2);
}
let string = '';
for(let i=1; i<=number; i++) {
string += `${calc(i)} `;
}
console.log(string);
}
fib(10)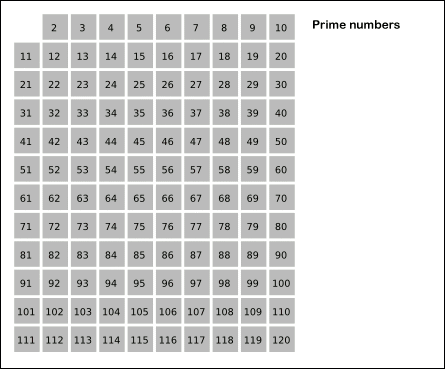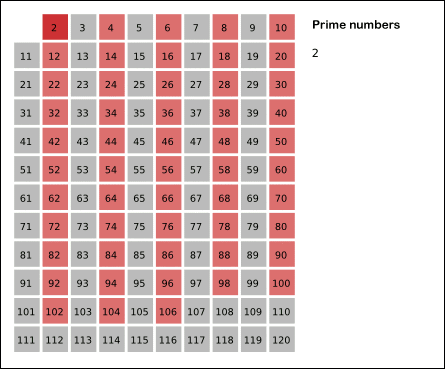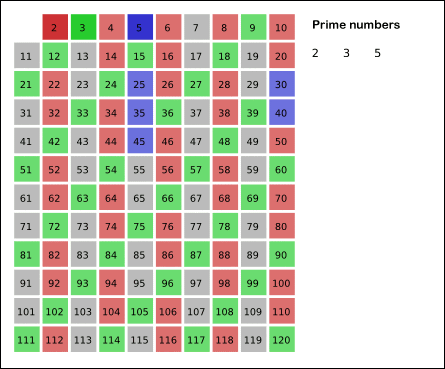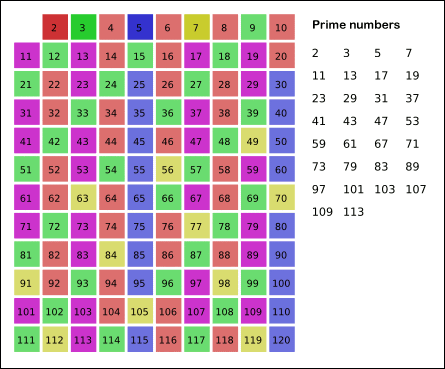
An ancient algorithm for finding all prime numbers up to a given number.
function soe(n) {
let a = []
let p = 2
for (let i=p; i<=n; i++) {
a.push(i)
}
console.log(compose(p, a, n).filter(m => m !== 0).join('-'));
}
function compose(p, a, n) {
if (p*p > n) {
return a
}
a = a.map(m => m!==p && m%p===0 ? 0 : m)
p = a.find(m => m!==0 && m>p)
return compose(p, a, n)
}
soe(100);Search a given value on properties of nested objects.
function search(obj, value) {
if (typeof obj !== 'object') {
return obj === value
}
for (const key in obj) {
if (obj.hasOwnProperty(key) && search(obj[key], value)) {
return true;
}
}
return false;
}
search({
level_1: {
level_2: {
level_3: {
level_4: {
level_5: {
value: 20
}
}
}
}
}
}, 20);Returns the leaf nodes of a given binary tree.
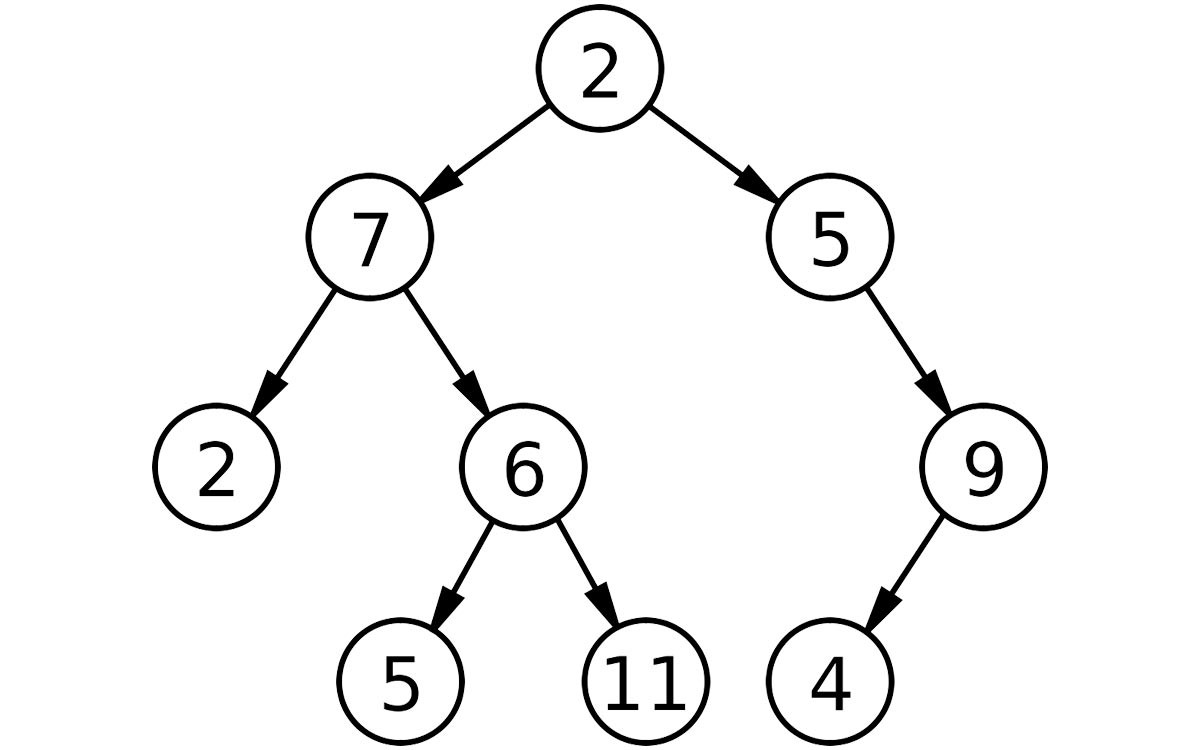
function search_leaf(tree) {
if (!tree.left && !tree.right) {
return tree.value
}
if (tree.left) {
let l = search_leaf(tree.left)
if (l) { console.log(l) }
}
if (tree.right) {
let l = search_leaf(tree.right)
if (l) { console.log(l) }
}
}
search_leaf({
"value": 8,
"left": {
"value": 3,
"left": {
"value": 1,
"left": null,
"right": null
},
"right": {
"value": 6,
"left": {
"value": 4,
"left": null,
"right": null
},
"right": {
"value": 7,
"left": null,
"right": null
}
}
},
"right": {
"value": 10,
"left": null,
"right": {
"value": 14,
"left": {
"value": 13,
"left": null,
"right": null
},
"right": null
}
}
});
Returns the leaf nodes on a Binary Search Tree.
function binary_search_tree(array) {
if (array.length===1) {
console.log(array[0]);
return;
}
const base = array[0]
const right = array.findIndex(n => n>base)
binary_search_tree(array.slice(1,right))
binary_search_tree(array.slice(right))
}
binary_search_tree([890,325,290,530,965]);
What is Domain Driven Design and why it is important to define a clear terminology? This article covers the key aspects of developing software following best practices of Domain Driven Design.
A basic but helpul introduction to Algorithm Complexity Analysis. An overview of tools for analysing algorithms and representing their complexity.
PM2 is a process manager for node.js applications. A powerful tool that will facilitate common system administration tasks for node apps.